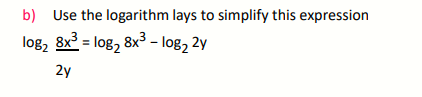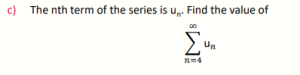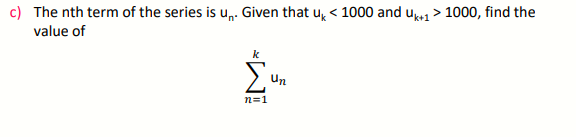- OTHM Level 5 K/650/1117 – Promoting Equality, Diversity, and Inclusion in Health and Social Care, Assignment, ILC, UK
- 7CO01: Critically evaluate underpinning theory and practice in this area and make recommendations for your organisation: Work and working lives in a changing business environment, Assignment, CIPD level 7, UK
- 7CO01: Evaluate the current trend for organisations to move from a five-day to a four-day working week without reducing their employees: Work and working lives in a changing business environment, Assignment, CIPD level 7, UK
- 7CO01: Critically discuss the current state of the major labour markets in which your organisation competes for staff in terms of both demand for and supply of skills: Work and working lives in a changing business environment, Assignment, CIPD level 7, UK
- 7CO01: Critically evaluate whether advancing technologies, and particularly artificial intelligence (AI): Work and working lives in a changing business environment, Assignment, CIPD level 7, UK
- Unit DAC4A1: Lead communication in adult care settings, Assignment, UOB, UK
- Unit HSC301: Role of the inter- professional team in delivering Health and Social care: An introduction to Health and Social Care, Assignment, UK
- Unit HSC301: The importance of regulatory bodies in delivery of high quality care: An introduction to Health and Social Care, Assignment, UK
- Unit HSC301: The main roles and responsibilities of Health and Social care workers when delivering care: An introduction to Health and Social Care, Assignment, UK
- Unit 04: Use an appropriate design tool to design a relational database system for a substantial problem: Database Design & Development, Assignment, BTEC Level 5, UK
- Unit 04: Centralized Database for MadZoo Digital-MadZoo Digital is a start-up company which was established in 2020: Database Design & Development, Assignment, BTEC Level 5, UK
- 5HR02: This unit focuses on the importance of effective workforce planning: Talent management and workforce planning, Assignment, CIPD, UK
- BMG847: Demonstrate a critical understanding of different research strategies and approaches: MSc International Business, Assignment, UU, UK
- Explain how the boundary layer thickness is defined- Give the definition of the friction coefficient: Thermofluids, Assignment, UOS, UK
- A thin-walled cylindrical pressure vessel with a diameter, D = 8 m, and an operational pressure 5 MPa made from a steel: Thermofluids, Assignment, UOS, UK
- Explain the physical importance and give the mathematical definition: Thermofluids, Assignment, UOS, UK
- 7HR01: Critically evaluating how this influences the work of its people professionals: Strategic employment relations, Assignment, CIPD, UK
- CIPD Level 3 3CO03: Ethical practice review A key responsibility for all ‘professionals’ is to regularly review and develop our performance at work: Core behaviours for people professionals, Assignment, UK
- CIPD Level 3: 3C002- Explain what evidence-based practice is and how it might be applied within an organisation: Principles of Analytics, Assignment , UK
- NVQ Unit 13 – Explain what it means to have a duty of care in your role and how it relates to duty of candour: The principles of Duty of Care, Assignment UK
MAST4001: Explain two different methods to solve a quadratic equation and what is meant by a real root: Algebraic Methods Assignment, UOK, UK
| University | University of kent (UOK) |
| Subject | MAST4001: Algebraic Methods |
Questions
a) Explain two different methods to solve a quadratic equation and what is meant by a real root. For each, describe an instance where it would be appropriate to use this method and give an example calculation.
b) Define the discriminant (sometimes known as determinant) of a quadratic equation and, using your own words, explain how it can be used to determine the number of solutions to the equation. Show example calculations to where one, two, or no real roots are found. Use hand-drawn or software-generated graphs to show the roots of the quadratic and indicate which roots are real.
c) Explain in your own words how to determine whether a geometric series will:
- converge
- diverge
- oscillate Define any algebraic variables you use.
d) Give an example of each type of series and carry out an example calculation to show that it converges, diverges, or oscillates.
You can either print out the document and answer on the sheet, or answer on separate paper. Once you’ve finished, either scan or clearly photograph your answers to upload them to your assignment.
1
2
a) Express x² + 4x – 7 in the form (x + p)² – q, where p and q are integers.
b) Hence, or otherwise, find the coordinates of the minimum point of the curve y = x² + 4x – 7.
3. The quadratic equation x² + (3k + 1)x + (4 – 9k), where k is constant, has repeated roots.
a) Show that 9k² + 42k – 15 = 0.
b) Hence find the possible values of k.
4.
a) Find the binomial expansion of (2 + 3x)5, simplifying the terms.
b) Hence find the binomial expansion of (2 + 3x)5 – (2 – 3x)5
5.
a) Evaluate and simplify the following logarithm to find x 2logb 5 + ½ log 9 − log 3 = logo x
c) The formula for the amount of energy E (in joules) released by an earthquake is E = (1.74 × 1019 × 101.44M) where M is the magnitude of the earthquake on the Richter scale.
i. The Newcastle earthquake in 1989 had a magnitude of 5 on the Richter scale. How many joules were released?
ii. In an earthquake in San Francisco in the 1900s the amount of energy released was double that of the Newcastle earthquake. What was its Richter magnitude?
6.
The first term of an infinite geometric series is 96. The common ratio of the series is 0.4.
a) Find the third term of the series.
b) Find the sum to infinity of the series.
7.
An arithmetic series has first term a and common difference d. The sum of the first ten terms of the series is 460.
a) Show that 2a + 9d = 92.
b) Given also that the 25th term of the sequence is 241, find the value of d.
Buy Answer of This Assessment & Raise Your Grades
Students Assignment Help UK offers the best Online Assignment Help to college students who wish to score top grades in their MAST4001: Algebraic Methods assignment. Our team of subject-oriented and highly qualified writers promises to deliver the best quality solution on engineering assignments at a discounted price.