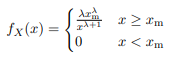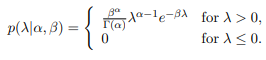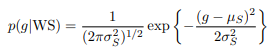AM41PB: Bayesian approach – The Pareto distribution is a power-law-like probability distribution that describes the distribution of wealth in a society: Probabilistic Modelling Coursework, UOM, UK

• Bayesian approach – The Pareto distribution is a power-law-like probability distribution that describes the distribution of wealth in a society, fitting the trend that a large portion of wealth is held by a small fraction of the population. It takes the form

where it provides the probability of x above a threshold Xm ≥ 0

On BlackBoard, under the section assignments, please find a dataset income distribution by percentile of the UK population for the tax years 2010-11 to 2018-9. Use the last digit of your student number to choose the tax year you will be working on (0 → 2010 − 11, 1 → 2011 − 2, . . . , 8, 9 → 2018 − 9).

1. Show that the Pareto distribution is indeed a probability distribution.
2. Plot the data as the percentage of the population (y-axis) with income above certain values (x-axis); to simplify the presentation present the income in thousands of pounds.
3. Assuming the data is i.i.d. and represented by the Pareto distribution, find the maximum likelihood expression for the parameter λML. Obtain the numerical value of λML given data D and Xm = £15, 000. Specify the data you are working with and the number of data points used.
4. For data set D = {x1, . . . , xN }, show that the Gamma probability distribution function
   
   is the conjugate prior for the Pareto distribution? Derive the corresponding posterior p(λ|D).
5. Assuming the data is represented by the Pareto distribution, find the Maximum A Posteriori expression of the parameter λMAP. Use the prior values α = 1 and β = 1 to obtain the numerical value of λMAP given data D.
6. Use the values obtained for the parameters λML and λMAP to compare the estimated percentage of the population with income above £20, 000.

• Decision theory- Large Diamonds (D) are exponentially rare and their weight follows the exponential distribution

where g is the weight of a diamond in grams and λD is a constant. In the same mine, there are also White Sapphire (WS) crystals that look like diamonds but are very regular in weight, following a Gaussian distribution.

of mean µS and variance σ, 2 S. The average size of diamonds λD is much smaller than that of White Sapphire λD << µS. Additionally, diamonds are much rarer, so p(WS) << p(D).

The mine owner wants to automate the sorting of Diamonds vs White Sapphire by weight, setting a threshold weight gT.

1. Write an expression for the misclassification error of Diamonds as White Sapphire p(D|WS) and of White Sapphire as Diamonds p(WS|D) as functions of the threshold weight gT.
2. Minimize the total misclassification error with respect to the threshold weight gT. What is the expression obtained for gT.
3. Calculate the value of gT for the parameters λD = 1, µS = 5, σ2 S = 1 and prior probabilities p(WS) = 0.8 and p(D) = 0.2. Sketch the two distributions, point to the threshold value gT and to the area that contributes to the misclassification error of Diamonds as White Sapphire.
4. The mine is losing money and the owner realizes that he has not taken into account that large diamonds are exponentially more expensive and the misclassification cost p(WS|D) with respect to p(D|WS) (which for simplicity we will attribute cost 1 to) is
   
   Assume λC < λD. Find the threshold weight gT expression in this case (not numerical value).

Answer

Request Answer of this Assignment