- K/650/1144 Professional Development and Academic Writing Skills Assessment
- M26753 Mechanical Principles Assignment Brief | University Centre IOW
- Care Safeguiding Children Assignment | Oxford Brookes University
- PSY4011 Developmental Psychology Assessment Brief | Arden University
- QSP7PCM Professional Cost Management Assignment 2 September 2025 | UCEM
- EGR2006M Control Systems Assignment 1 Brief | University of Lincoln
- MBA7066 Innovation and Entreprenuership Assignment Portfolio 2025 | UGM
- Contract Law Assessment 2 Problem Scenario 2025-26 | University Of Salford
- Operations & Supply Chain Management Assignment Brief : E-Commerce Supply Chain Efficiency
- Unit 1 Programming Assignment 2025-26 | ESOFT Metro Campus
- K/651/4745 Unit 1 Teaching My Subject Written Assignment | Britannia Education Group
- H/650/1099 Level 4 Academic Writing and Research Skills Assignment Brief | LSBU
- ASB-4012 Codding for Business Application Assignment – Project in R | Bangor University
- Unit: Team Management in Health and Social Care OTHM Level 5 Diploma Assignment
- BTEC Level 3 Unit 4 Programming Assignment – Concepts of Programming
- HSO4004 Principles of Care Assignment-1 and Assignment-2 Semester-1 September 2025-26
- 1031ENG-N Civil Engineering Construction Technology In-Course Assessment (ICA) Group Report | Teesside University (TU)
- MOD009382 Finance and Governance in Health and Social Care 011 Assessment Coursework Report | Anglia Ruskin University
- Geotechnical Engineering Assignment 2025/26 – University Of Surrey (UniS)
- Essentials of Adult Nursing Summative Assessment – University of Roehampton London (UoRL)
BTEC Level 5 Unit 5006 Further Mathematics Assignment 2025-2026 | UCL
| University | University Centre Leeds (UCL) |
| Subject | Unit 5006 Further Mathematics |

Unit 5006 2025-26
INTRODUCTION
The understanding of more advanced mathematics is important within an engineering curriculum to support and broaden abilities within the applied subjects at the core of all engineering programmes. Students are introduced to additional topics that will be relevant to them as they progress to the next level of their studies, advancing their knowledge of the underpinning mathematics gained in Unit 4002: Engineering Maths.
The unit will prepare students to analyse and model engineering situations using mathematical techniques. Among the topics included in this unit are: number theory, complex numbers, matrix theory, linear equations, numerical integration, numerical differentiation, and graphical representations of curves for estimation within an engineering context. Finally, students will expand their knowledge of calculus to discover how to model and solve engineering problems using first and second order differential equations. On successful completion of this unit students will be able to use applications of number theory in practical engineering situations, solve systems of linear equations relevant to engineering applications using matrix methods, approximate solutions of contextualised examples with graphical and numerical methods, and review models of engineering systems using ordinary differential equations
DELIVERY
The main mode of delivery of this 60 hours module is lectures supported by classroom exercises and worked examples. The material discussed during class will be available on Google Classroom for self-study and will be complemented by preparatory learning material.
Students are expected to attend all teaching sessions and to submit work on time. It is expected that students should allocate approximately 150 study hours per module (for a 15 credit module). This will include lectures and tutorials, VLE based activities, research and assessment preparation and submission.
If for some reason you are unable to attend then you must inform your module tutor. In cases of illness you should also provide a doctor’s note.
You are expected to meet submission deadlines detailed in this handbook. For information on the penalties for late/non submission please see the Academic Regulations which can be found on the VLE.
TUTOR
Dr Md Akmol Hussain is the Programme Manager for Engineering at University Centre Leeds. He holds a teaching qualification (PGCE) with Qualified Teacher Status, as well as over 10 years of experience teaching a wide range of engineering courses – including Electrical/Electronics, Robotics, Engineering Maths and PLCs – at various levels, from Level 3 to degree. He also holds a PhD in Computer Vision, a Postgraduate Certificate (research-based), a B.Eng in Electronics and Communication Engineering, and an HND in Electrical and Electronics Engineering, providing him with a solid academic and practical foundation.
Dr Hussain has published 4 high impact journal articles in IEEE Access, 6 conference papers, and a book chapter. His research focuses on digital image and video processing, and control engineering, particularly the design and implementation of automated systems through programming and algorithm development.
Contact details:
Email:
Phone:
Do You Need Assignment of This Question
MODULE SPECIFICATION
LO1 Use applications of number theory in practical engineering/manufacturing situations.
Number theory:
- Bases of a number (Denary, Binary, Octal, Duodecimal, Hexadecimal) and converting between bases.
- Types of numbers (Natural, Integer, Rational, Real, Complex.)
- The modulus, argument, and conjugate of complex numbers.
- Polar and exponential forms of complex numbers.
- The use of de Moivre’s Theorem in engineering/manufacturing
- Complex number applications e.g., electric circuit analysis, information, and energy control systems.
- Application of advanced numerical skills (Binary, dotted decimal notation) required to meet the defined specifications.
- Problem-solving and ensuring quality solutions to practical.
- engineering/manufacturing situations relevant to the occupation/sector.
- (e.g., operations, manufacturing, space, aeronautical, automation, electrical, electronics, mechanical, etc.); attention to detail and responsive to feedback; communication and presentation of solutions (including written, verbal, electronic format) to stakeholders, discussions, and negotiations.
LO2 Solve systems of linear equations relevant to engineering/manufacturing applications using matrix methods.
Matrix methods:
- Introduction to matrices and matrix notation.
- The process for addition, subtraction, and multiplication of matrices Introducing the determinant of a matrix and calculating the determinant for a 2×2 and 3×3 matrix.
- Using the inverse of a square matrix to solve linear equations.
- Cramers Rule Gaussian elimination to solve systems of linear equations (up to 3×3) Eigenvalues and Eigenvectors.
LO3 Approximate solutions of contextualised examples with graphical and numerical methods.
Graphical and numerical methods:
- Standard curves of common functions, including quadratic, cubic, logarithm, and exponential curves.
- Systematic curve sketching knowing the equation of the curve.
- Using sketches to approximate solutions of equations.
- Numerical analysis using the bisection method and the Newton–Raphson Method.
- Numerical integration using the mid-ordinate rule, the trapezium rule, and Simpson’s rule.
- Examples of engineering scenarios using numerical methods for first-order and second-order differential equations; partial differential equations; homogeneous and non-homogeneous equations.
LO4 Review models of engineering/manufacturing systems using ordinary differential equations.
Differential equations:
- Formation and solutions of first-order differential equations (e.g., separation of variables)
- Applications of first-order differential equations e.g., RC and RL electric circuits,
- Newton’s laws of cooling, charge and discharge of electrical capacitors, and complex stresses and strains
- Formation and solutions of second-order differential equations
- Applications of second-order differential equations e.g., mass-spring-damper systems, information and energy control systems, heat transfer, automatic control systems and beam theory and RLC circuits
- Introduction to Laplace transforms for solving linear ordinary differential equations
- Applications involving Laplace transforms and inverse Laplace transforms.
- For example, electric circuit theory, load frequency control, harmonic vibrations of beams, reactor dynamics, and engine governors.
SCHEME OF WORK
| Week no. | Date (w/c) | Topic | Advance Reading | Deadlines |
| 1 | 15/09/2025 | LO1-4/ Introduction and general number theory | (video, internet resources), (video, internet resources), (videos, ) | |
| 2 | 22/09/2025 | LO1/ Complex number and their mathematical operation (incl Moivre’s Theorem) | www.mathcentre.ac.uk
| |
| 3 | 29/09/2025 | LO1/ Application of complex numbers (I) | SINGH, K. (2011) Engineering Mathematics Trough Applications. Basingstoke, Palgrave Macmillan. | |
| 4 | 06/10/2025 | LO1/ Application of complex numbers (II) | Review: M1 | |
| 5 | 13/10/2025 | LO2/ Introduction to matrices and their mathematical operations | ||
| 6 | 20/10/2025 | LO2/ Determinant of matrix and inverse of square matrix
| STROUD, K.A. and BOOTH, D.J. (2013) Engineering Mathematics. 7th Ed: Basingstoke, Palgrave Macmillan. | |
| 27/10/2025 | Reading Week | Review: M2 | ||
| 7 | 03/11/2025 | LO2/ Using matrices to solve linear equations (incl Gaussian elimination) | Final: M1, M2 | |
| 8 | 10/11/2025 | LO3/ Graphical method to determine solution of a problem | ||
| 9 | 17/11/2025 | LO3/ Numerical analysis (two methods to find roots and differential equations) | BIRD, J. (2014) Higher Engineering Mathematics. 7th Ed. London: Routledge. | |
| 10 | 24/11/2025 | LO 3/ Numerical integration (two methods) | ||
| 11 | 01/12/2025 | LO4/ First order differential equation and their application | Review: M3 | |
| 12 | 08/12/2025 | LO4/ Second order differential equation and their application | ||
| 13 | 15/12/2025 | LO4/ Laplace transforms and their applications | Review: M4 | |
| 22/12/2025 | Christmas Holidays | |||
| 29/12/2025 | Christmas Holidays | |||
| 14 | 05/01/2026 | Revision | Final: M3, M4 | |
| 15 | 12/01/2026 | Review and module evaluation |
Buy Answer of This Assessment & Raise Your Grades
HIGHER EDUCATION ASSESSMENT FRONT SHEET
Pearson BTEC Level 5 Higher National Diploma in Electrical and Electronic Engineering/Manufacturing Engineering
| COURSE TITLE | Pearson BTEC Level 5 Higher National Diploma in Electrical and Electronic Engineering/Manufacturing Engineering | ||
| STUDENT NAME | |||
| MODULE TITLE | Unit 5006: Further Mathematics | ||
| TITLE OF ASSIGNMENT | FM1: Number theory FM2: Matrix methods | ||
| DEADLINE DATE FOR SUBMISSION BY STUDENTS | 03/11/2025 | ||
| ISSUE DATE | 15/09/2025 | ||
| FORMATIVE FEEDBACK DATE | 27/10/2025 | ||
| SUBMISSION LOCATION | Turnitin | ||
| ASSESSOR(S) | Md Akmol Hussain | ||
| IV NAME | Arshad Mir | ||
LEARNING OUTCOMES ASSESSED
LO1 Use applications of number theory in practical engineering situations
LO2 Solve systems of linear equations relevant to engineering applications using matrix methods
NOTES FOR STUDENTS
What is Academic Malpractice?
Academic malpractice relates to academic work that does not meet normal standards of academic practice and encompasses all kinds of academic dishonesty, whether deliberate or unintentional, which infringes the integrity of the College’s assessment procedures. ‘Candidate malpractice’ means malpractice by a candidate in the course of any examination or assessment, including the preparation and authentication of any controlled assessments or coursework, the presentation of any practical work, the compilation of portfolios of assessment evidence and the writing of any examination paper.
| Learner declaration (authentication) |
| I certify that the work submitted for this assignment is my own and research sources are fully acknowledged. Student signature: Date: |
Assessment Brief
| Student Name/ID Number | |
| Unit Number and Title | Unit 5006: Further Engineering Mathematics |
| Academic Year | 2025/26 |
| Unit Tutor | Md Akmol Hussain |
| Assignment Title | FM1: Number theory |
| Review date | 20/10/25 |
| Submission Date | 03/11/25 |
| IV Name | Arshad Ahmed Mir |
Submission Format
This assignment can be either handwritten or typed in full, but all the working must be shown in order to demonstrate your understanding of the tasks. It is recommended that students make a copy of their assignment for their own records if it is handwritten.
L01 Use applications of number theory in practical engineering situations
Assignment Brief and Guidance
Scenario:
You work as an engineer at a multinational manufacturing organisation, they have just taken on some new engineering apprentices. The research and development department has requested your assistance of the design of a manual containing set worked questions and their associated advanced mathematical techniques, which are likely to be consulted by their aspiring engineers in developing solutions to real problems. Therefore, solve the following task describing your thought process.
Task 1
a. Convert the following numbers into decimals. These bases are frequently used in computer engineering:
- 110011002
- 59014388
- 43A62C16
b. Multiply the following numbers:
- A516 * 248
- A12Hex * F8Hex
Task 2
The impedances Z1 and Z2 in an electric circuit are in series. What is the total impedance? State your answer in polar and rectangular forms.
● Z1 = (15 + j 10) Ω
● Z2 = 40 Ω
Task 3
- A system has an open-loop transfer function (G) given by:
G = 7 ej2π * 1.02 ej0.2 / 1.8 ej0.99
Simplify G.
- Express the following current in complex exponential form:
i(t) = 30cos (100t – 60°)
Task 4
Find a formula for cos (3θ) in terms of cos (θ) and sin (θ) using de Moivre’s theorem
Learning Outcomes and Assessment Criteria | |||
| Learning Outcome | Pass | Merit | Distinction |
| LO1 Use applications of number theory in practical engineering situations. | P1 Apply addition and multiplication methods to numbers that are expressed in different base systems.
P2 Solve engineering problems using complex number theory.
P3 Perform arithmetic operations using the polar and exponential form of complex numbers. | M1 Deduce solutions of problems using de Moivre’s Theorem. | D1 Test the correctness of a trigonometric identity using de Moivre’s Theorem. |
Are You Looking for Answer of This Assignment or Essay
Assessment Brief
| Student Name/ID Number | |
| Unit Number and Title | Unit 5006: Further Engineering Mathematics |
| Academic Year | 2025/26 |
| Unit Tutor | Md Akmol Hussain |
| Assignment Title | FM2 – Matrix Methods |
| Review date | 20/10/2025 |
| Submission Date | 03/11/2025 |
| IV Name | Arshad Ahmed Mir |
Submission Format
Instruction to students:
● To maximise your learning outcome, attempt all tasks in this assignment.
● Submit your assignment with your signed front sheet (for authentication) to TurnItIn.
LO2 Solve systems of linear equations relevant to engineering applications using matrix methods
Assignment Brief and Guidance
Scenario:
ou are working as an engineer for a multinational manufacturing organisation who has just taken on some new apprentices. The research and development department has requested your assistance in the design of a booklet containing set worked engineering questions and their associated advanced mathematical techniques. This training booklet will be used aspiring engineers by developing solutions to real world problems. Therefore, solve the following tasks and describing your thought process.
Task 1:
Calculate the determinant of the matrix A.
| 1 | 2 | 7 | |
| det A = | 0 | 4 | 2 |
| 2 | -1 | 3 |
Task 2:
Solve the system of the three linear equations shown below using Gaussian elimination.
| (eq. 1) | 2 x1 | – | 2 x2 | + | 2 x3 | = | 0 |
| (eq. 2) | 8 x1 | + | 10 x2 | + | 2 x3 | = | 6 |
| (eq. 3) | -2 x1 | + | x2 | – | 3 x3 | = | 5 |
Task 3:
Determine the solutions to the set of engineering linear equations below by using the Inverse Matrix Method for a 3×3 matrix.
x + 2y +3z = 5
2x -3y -z = 3
-3x +4y + 5z = 3
Task 4:
Write a report on the analytical matrix solutions by:
– Briefly describing them.
– Evaluate your given solutions computed in this assignment by using these methods with appropriate computer software.
Learning Outcomes and Assessment Criteria | |||
| Learning Outcome | Pass | Merit | Distinction |
| LO2 Solve systems of linear equations relevant to engineering applications using matrix methods
| P4 Ascertain the determinant of a given 3×3 matrix. P5 Solve a system of three linear equations using Gaussian elimination.
| M2 Determine solutions to a set of linear equations using the Inverse Matrix Method.
| D2 Evaluate and validate all analytical matrix solutions using appropriate computer software.
|
Do You Need Assignment of This Question
Pearson BTEC Level 5 Higher National Diploma in Electrical and Electronic Engineering/Manufacturing Engineering
| COURSE TITLE | Pearson BTEC Level 5 Higher National Diploma in Electrical and Electronic Engineering/Manufacturing Engineering | ||
| STUDENT NAME | |||
| MODULE TITLE | Unit 5006: Further Engineering Mathematics | ||
| TITLE OF ASSIGNMENT | FM3: Graphical and numerical methods FM4: Differential equations | ||
| DEADLINE DATE FOR SUBMISSION BY STUDENTS | 05/01/2026 | ||
| ISSUE DATE | 15/09/2025 | ||
| FORMATIVE FEEDBACK DATE | 29/12/2025 | ||
| SUBMISSION LOCATION | Turnitin | ||
| ASSESSOR(S) | Md Akmol Hussain | ||
| IV NAME | Arshad Ahmed Mir | ||
| LEARNING OUTCOMES ASSESSED LO3: Approximate solutions of contextualised examples with graphical and numerical methods LO4: Review models of engineering systems using ordinary differential equations | |||
NOTES FOR STUDENTS
What is Academic Malpractice?
Academic malpractice relates to academic work that does not meet normal standards of academic practice and encompasses all kinds of academic dishonesty, whether deliberate or unintentional, which infringes the integrity of the College’s assessment procedures. ‘Candidate malpractice’ means malpractice by a candidate in the course of any examination or assessment, including the preparation and authentication of any controlled assessments or coursework, the presentation of any practical work, the compilation of portfolios of assessment evidence and the writing of any examination paper.
| Learner declaration (authentication) |
| I certify that the work submitted for this assignment is my own and research sources are fully acknowledged. Student signature: Date: |
Assessment Brief
| Student Name/ID Number | |
| Unit Number and Title | Unit 5006: Further Engineering Mathematics |
| Academic Year | 2025/26 |
| Unit Tutor | Md Akmol Hussain |
| Assignment Title | FM3: Graphical and numerical methods |
| Review date | 22/12/2025 |
| Submission Date | 05/01/2026 |
| IV Name | Arshad Ahmed Mir |
| Submission Format |
| Instruction to students: ● To maximise your learning outcome, attempt all tasks in this assignment. ● Submit your assignment with your signed front sheet (for authentication) to TurnItIn. |
LO3: Approximate solutions of contextualised examples with graphical and numerical methods
Assignment Brief and Guidance
Scenario
You are working as an engineer for a multinational manufacturing organisation who has just taken on some new apprentices. The research and development department has requested your assistance in the design of a booklet containing set worked engineering questions and their associated advanced mathematical techniques. This training booklet will be used aspiring engineers by developing solutions to real world problems. Therefore, solve the following tasks and describing your thought process.
Task 1
In operations research, the solutions to problems can frequently be estimated with graphical methods. In this task you have to maximise the profit (Z). The relationship with two other variables (x, y) as well as their constraints is shown below:
Z = 3x + 10y
Constraints: 2x + 5y16, x0, y 0 and x5.
Task 2
A ball is drifting on the surface of the water (see Figure below). The question investigated here is: If the radius and water density are known, how deep does the ball sink in?

Figure 1: Drifting ball
The approach is centred around the fact that the buoyancy and gravity are in equilibrium and, therefore, the following equation needs to be solved for x, and the roots be determined. Use both the bisection method and the Newton–Raphson method to perform this task (i.e first, find the roots using bisection method, then use newton-raphson method to also find the roots). Conduct the number of iterations required to achieve an error tolerance ∊ ≤ 0.05%.
Where:
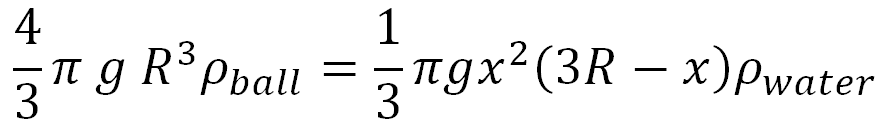
g: Gravitational constant
R: Radius of ball
ρball: Density of ball (500 kg/m3)
ρwater: Density of water (1000 kg/m3)
Task 3
Determine the approximate value of the following integral using two different numerical integral methods.
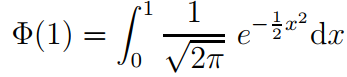
Task 4
The charging of a capacitor through a resistor can be modelled by a first order differential equation. Develop a model for the capacitor voltage (assume no prior charge) for a step input of 5 V (at t =0), a capacitor of 20μF and resistor of 850Ω. Graph the capacitor voltage for the first five time constants.
Write an essay critiquing the use of numerical estimation methods, commenting on their applicability and the accuracy of the methods. (Suggested word count: 500 words, use at least two textbook references)
Learning Outcomes and Assessment Criteria | |||
| Learning Outcome | Pass | Merit | Distinction |
| LO3 Approximate solutions of contextualised examples with graphical and numerical methods
| P6 Estimate solutions of sketched functions using a graphical estimation method P7 Calculate the roots of an equation using two different iterative techniques P8 Determine the numerical integral of engineering functions using two different methods
| M3 Solve engineering problems and formulate mathematical models using first-order differential equations
| D3 Critique the use of numerical estimation methods, commenting on their applicability and the accuracy of the methods.
|
Buy Answer of This Assessment & Raise Your Grades
Assessment Brief
| Student Name/ID Number | |
| Unit Number and Title | Unit 5006: Further Engineering Mathematics |
| Academic Year | 2025/26 |
| Unit Tutor | Md Akmol Hussain |
| Assignment Title | FM4: Differential Equations |
| Review date | 22/12/2025 |
| Submission Date | 05/01/2026 |
| IV Name | Arshad Ahmed Mir |
| Submission Format |
| Instruction to students: ● To maximise your learning outcome, attempt all tasks in this assignment. ● Submit your assignment with your signed front sheet (for authentication) to TurnItIn. |
LO4: Review models of engineering systems using ordinary differential equations
Assignment Brief and Guidance |
Scenario
You are working as an engineer for a multinational manufacturing organisation who has just taken on some new apprentices. The research and development department has requested your assistance in the design of a booklet containing set worked engineering questions and their associated advanced mathematical techniques. This training booklet will be used aspiring engineers by developing solutions to real world problems. Therefore, solve the following tasks and describing your thought process
Task 1
The cooling of metal in the annealing process can be approximated using Newton’s cooling law: dT/dt = –k (T–Tamb). If the cooling process follows the dashed-dotted, (red) line in Figure 1, review value k for a θamb = 20°C.
Figure 1: Cooling experiments of a cylindrical sample from EN AW-6082 in a gas nozzle field and in calm air and approximation of the temperature development with Newtonian law of cooling. (Milkereit, 2011)
Task 2
The motion of a pendulum can be modelled with a second order differential equation of the form: d2x/dt2 + α x = 0, where x is the distance of the pendulum mass from the position of rest. Show that α is the square of the angular frequency ω. If x(t) = Xo cos(ωt), where Xo= x(0) (Xo ≠ 0)
Task 3
The diagram displays the behaviour of the mass-spring-damper system shown in Figure 2 can be described by mx’’ + bx’ + kx = F.
Figure 2: Mass-spring-damper system
Use Laplace transforms to calculate the unit step response to such a system if m = 1 kg, b = 10 Ns/m, k = 16 N/m.
Task 4
Write an essay (suggested word count: 750 words) evaluating how different models of engineering systems using first-order differential equations to solve engineering problems (choose two examples to illustrate).
Task 5
Write an essay (suggested word count: 750 words) to critically evaluate first and second-order differential equations when generating the solutions to engineering situations using models of engineering systems.
Learning Outcomes and Assessment Criteria | |||
| Learning Outcome | Pass | Merit | Distinction |
| LO4 Review models of engineering systems using ordinary differential equations
| P9 Determine first order differential equations and their application to engineering systems using analytical methods. P10 Determine second-order homogeneous and nonhomogeneous differential equations and their application to engineering systems using analytical methods. P11 Calculate solutions to linear ordinary differential equations using Laplace transforms. | M4 Evaluate how different models of engineering systems using first-order differential equations solve engineering problems.
| D4 Critically evaluate first and second-order differential equations when generating the solutions to engineering situations using models of engineering systems.
|
Recommended Resources
Note: See HN Global for guidance on additional resources.
Print Resources
- Arfken G. B., Weber H. J., and harris F. E. (2011) Mathematical methods for physicists: a comprehensive guide. Academic press.
- Bird J. (2021) Higher Engineering Mathematics. 9th Ed. Routledge.
- Bird J. (2019) Science and Mathematics for Engineering. 6th Ed. Routledge.
- Botelho F.S. (2021) Functional Analysis, Calculus of Variations and Numerical Methods for Models in Physics and Engineering. 1st Edition. CRC Press.
- Chapra S. (2022) Applied Numerical Methods with MATLAB for Engineers and Scientists.
- 5th Edition. McGraw-Hill.
- Chapra S. and Clough D. (2021) Applied Numerical Methods with Python for Engineers and Scientists. 1st Edition. McGraw-Hill.
- Chapra S. and Canale R. (2020) Numerical Methods for Engineers. 8th Edition. McGraw-Hill.
- Croft A., Davison R., Hargreaves M., and Flint J. (2017) Engineering Mathematics.
- 5th edition. Pearson Education.
- Duffy D.G (2022) Advanced Engineering Mathematics: A Second Course with MatLab.
- 1st Edition. CRC Press.
- Glyn J. and Dyke P. (2020) Modern Engineering Mathematics. 6th edition. Pearson.
- Islam N., Singh S.B., Ranjan P., and Haghi A.K. (2021) Mathematics Applied to Engineering in Action: Advanced Theories, Methods, and Models. 1st Edition. CRC Press.
- Made Easy Editorial Board (2022) Engineering Mathematics for GATE 2023 and ESE 2023
- (Prelims) – Theory and Previous Year Solved Papers. India: Made EASY Publications Pvt Ltd.
- Ram M. (2021) Recent Advances in Mathematics for Engineering. CRC Press.
- Teodorescu P., Stanescu N., and Pandrea N. (2013) Numerical Analysis with Applications in Mechanics and Engineering. Wiley-IEEE Press.
- Ram M. (2020) Mathematics in Engineering Sciences: Novel Theories, Technologies, and Applications. 1st Edition. CRC Press.
- Vick B. (2020) Applied Engineering Mathematics. CRC Press.
- Singh K. (2011) Engineering Mathematics Trough Applications. Basingstoke, Palgrave Macmillan.
- Stroud K.A. and Booth D.J. (2013) Engineering Mathematics. 7th Ed: Basingstoke, Palgrave Macmillan.
Are You Looking for Answer of This Assignment or Essay
Working on your Unit 5006 Further Mathematics Assignment at University Centre Leeds? Many engineering students find number theory, matrix methods, and differential equations challenging. Our experts at Student Assignment Help UK provide clear, AI-free electrical and electronic engineering assignment solutions. Get trusted Engineering Assignment Help UK today and score higher with confidence.




