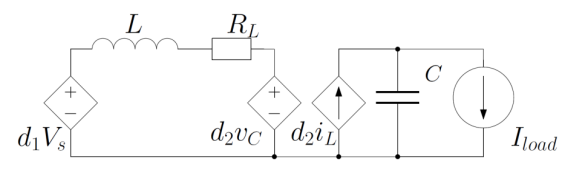
Derive and write the averaged model of the DC-DC Buck-Boost converter, as described in Figure: Intelligent Systems & Control Assignment, DMU, UK

Questions:

Part A:

1. Derive and write the averaged model of the DC-DC Buck-Boost converter, as described in Figure. Consider as the measured output of the system the output voltage, equivalently, the voltage of the capacitor C).
   
2. Linearise the model around the equilibrium point xeq=[20 0.4]T and derive the linearised state space representation.
3. Provide several simulations of the averaged, nonlinear model and the linearised model you have acquired from questions 1 and 2 around the equilibrium point. Start by having as the initial condition the equilibrium point, and gradually use initial conditions that are farther away from it. You can use as constant input the input vector corresponding to the equilibrium point. Plot the time responses of the states for the two models against each other. Also, plot the trajectories of each model in the state space. Observe and report the differences, if any.
4. Assuming a zero-order-hold discretization scheme, derive the discretized system from the linearised system, for a sampling period T=10μsecs. Compare the discretized version with the continuous-time system in a simulation, where the discretized system and the continuous-time linearised system are plots in the same figure.
5. Compare also the state coming from the discrete approximation using Euler forward difference acting on the nonlinear system, i.e., by setting
   

Part B:

1. Is the linearised continuous system controllable?
2. Using the continuous-time linearised model, develop a stabilizing state space control law that drives the system to the equilibrium point. The closed-loop system must have a damping factor ζ=0.86 and a damped natural frequency ωd=2000.
3. Simulate the open-loop linearised system and the closed-loop linearised system, and the closed-loop averaged system, for two initial conditions and observe/highlight the differences in the responses. Justify your choice of initial conditions.

Part C:

1. The inductor current iL cannot be measured accurately without an expensive sensor. Thus, the controller designed in Part B cannot be implemented without an additional cost. To avoid this, we can develop an observer that estimates both states of the linearised system. Choose the eigenvalues of the closed-loop error dynamics of the observer and justify your decision.
2. Write down the complete observer equation, that is the closed-loop error dynamics and the state estimate dynamics.

Part D:

1. Consider the controller designed in Part B, which uses the state estimation instead of the actual states, as designed in Part C. Derive the resulting closed-loop system and write down the state equations and output equations. Is the resulting closed-loop system stable and why?
2. Simulate two closed-loop systems with the controller designed in Part B by (i) taking the actual state as feedback and (ii) taking the state estimation as feedback. Observe differences if any.

Answer

Request Answer of this Assignment