- UMACTF-15-M: You have recently been appointed as a Financial Analyst for a leading investment bank in London: Corporate Financial Strategy Course Work, UWE, UK
- BAM5010: choose an organisation and make some recommendations for the delivery: Work Based Project Course Work, UOB, UK
- You are required to calculate ratios for Fresh Farms Ltd: financial Course Work, UK
- Understand the legal, ethical and theoretical context for health, safety and risk management: leadership and Management Course Work, UK
- P3 Describe the types of training and development used by a selected business: BTEC Business Extended Diploma Pearson Course Work, UK
- Describe how a selected business identifies training needs: BTEC Business Extended Diploma Pearson Course Work, UK
- Discuss your chosen business, background information and why you have chosen that business: BTEC Business Extended Diploma Pearson Course Work, UK
- Activity 7: Risk management in an organisation should be both sensible and proportionate to the level of risk involved: NEBOSH IDIP ID1 Research Paper Course Work, OU, UK
- Activity 6: Reviewing health and safety performance Critique your chosen organisation’s health and safety: NEBOSH IDIP ID1 Research Paper Course Work, OU, UK
- Activity 5: Management of contractors Review how your chosen organisation selects contractors and manages them while they are on site: NEBOSH IDIP ID1 Research Paper Course Work, OU, UK
- Activity 2: Preparing a brief research report on approaches to worker consultation: NEBOSH IDIP ID1 Research Paper Course Work, OU, UK
- Create an organisational risk profile for your chosen organisation: NEBOSH IDIP ID1 Research Paper Course Work, OU, UK
- Explain the differences between learning requirements and continuous professional development: Leadership and Management Assignment, UL, UK
- What steps, component parts and enabling tools would you use to develop a therapy: Advanced therapeutic medicinal products Course Work, TUM, UK
- CS3DS19: Construct a KNIME workflow to understand the data characteristics and quality, report: Data Science Algorithms and Tools Course Work, UOW, UK
- Explain how principles of support are implemented in health and social care practice: Diploma In Health And Social Care Level 5 Course Work, UK
- The UK Manufacturing UK LTD is facing an array of issues that require a sound understanding: Management Decision Making Assignment, USM, UK
- Identify sources of information and guidance about how to support a child or young person: child care diploma level 3 Course Work, OU, UK
- Explain why it is important to take full account of a child or young person’s level of understanding: Child care diploma level 3 Course Work, OU, UK
- Understand how to support children and young people who have experienced harm or abuse: child care diploma level 3 Course Work, OU, UK
MATH1145: You are asked to calculate the distance covered by the vehicle in the time between 0 and 10 seconds both by analytical integration (exact solution) and by 5 different numerical integration approximations: Engineering Mathematics Coursework, UOG, UK
| University | University of Greenwich (UOG) |
| Subject | Engineering Mathematics |
MATH1145 – Engineering Mathematics II
Mathematical analysis and MATLAB modelling coursework Mechanical Engineering, Academic year: 2020-2021
Use the template provided on Moodle to prepare your submission. Submission Deadline: Upload your individual reports by 2nd April 2021, 11:30 pm
For more information about the Rubric, refer to the Assessment details document on Moodle.
Do You Need Assignment of This Question
TASK 1: numerical integration and differentiation tasks (40%)
a) The velocity of a vehicle, for 0 ≤ 𝑡 ≤ 10𝑠𝑒𝑐 is described by the function:
𝑣(𝑡) = 50 + (𝑐 + 1) × 𝑡 × cos (𝑡) (km/h), where c is the last digit of your student ID. You are asked to calculate the distance covered by the vehicle in the time between 0 and 10 seconds, both by analytical integration (exact solution) and by 5 different numerical integration approximations:
i) The 3 Riemann sums (left, right & midpoint)
ii) The trapezoidal rule, and
iii) The Simson’s Rule, and demonstrate how each of these methods converges to the exact solution, as you increase the number of the sub-intervals you will use to discretise the time interval t[0,10]. Reflect on the results.
b) Insert the discrete acceleration time history ‘THS_0c’ (where c is the last digit of your student ID) in MATLAB and apply any valid numerical integration method to calculate the velocity and displacement time histories. Then apply any numerical differentiation technique to the displacement time history to go back to velocity and acceleration. Comment on the results or any discrepancies you observe.
Extra task: Try to use less discrete points for the displacement time history (re-sample, e.g. one every 2, every 4 or every 5 points), and differentiate again. Compare and reflect on the results.
TASK 2: Application of ODEs into the analysis of a beam (60%)
Consider a beam with an inverted tee-shaped cross-section which is made of stainless steel (𝐸 = 210𝐺𝑃𝑎) and it is fixed in one end and supported on a pin on the other end, as shown in the figure. The beam is subject to a uniformly distributed load 𝑞0 along its whole length.
a) Develop the ODE of the problem. Solve the ODE to get the analytical solution.
b) Solve the ODE applying a Finite differences stencil, until you achieve satisfactory agreement with the analytical solution. Show the formulation of the equations and program them in MATLAB. Select any method you prefer to solve the linear system of equations.
c) Write a MATLAB code that locates the centroid axes of the cross-section
d) Write a MATLAB code that determines the moment of inertia of the cross-section
e) Apply a suitable numerical analysis to calculate the bending moment and shear force diagrams along the axis of the beam
f) Write a MATLAB code to determine the maximum bending moment and for this moment calculates the stress at points K and H in the cross-section
Cross-section of the beam
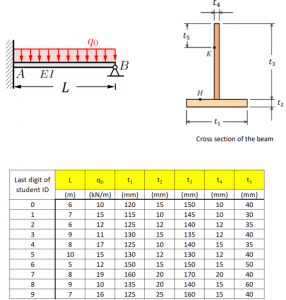
Table 1 Parameters for your analysis
Buy Answer of This Assessment & Raise Your Grades
Grab the faultless coursework writing service UK by the StudentsAssignmentHelp.co.uk. Our coursework writers have amazing skills to prepare fresh and original coursework answers on engineering assignments at a cheap price.
Answer
