Identify the Relevance of Mathematical Methods to a Variety of Conceptualized Engineering Examples: Engineering Mathematics Assignment, ICL, UK

Unit Learning Outcomes

LO1: Identify the relevance of mathematical methods to a variety of conceptualized engineering examples.
LO2: Investigate applications of statistical techniques to interpret, organize and present data.
LO3: Use analytical and computational methods for solving problems by relating sinusoidal wave and vector functions to their respective engineering applications.
LO4: Examine how differential and integral calculus can be used to solve engineering problems.

Scenario:
As an electrical and electronic engineer, you always encounter equations, problems, and data that need to be analyzed in order to understand the results in a practical way. You are working as an engineer and you have completed many tasks in a job that you were asked to carry out. A report must be prepared for your senior in order to analyze the results that you have obtained in your experiments. You must analyze the results carefully using the methodologies that you have learned in engineering maths. Your report must be clear and presented in a professional way as this will have a major impact on how well you impress your superiors and obtain the promotion that you have been working for a long time. All the tasks must be finalized on time and the analysis must be thorough and convincing.

LO1: Identify the relevance of mathematical methods to a variety of conceptualized engineering examples.

a- The speed of sound in gas might plausibly depend on the pressure Ρ, the density �, and the volume of the gas. Use dimensional analysis to determine the exponents, � and � in the formula. where is a dimensionless constant?
Incidentally, the units of pressure are kilograms per meter per second squared.

b- Force of viscosity F acting on a spherical body moving through a fluid depends upon its velocity (v), radius (r), and coefficient of viscosity ‘η’ of the fluid. Using the method of dimensions obtains an expression for ‘F’.

c- An arithmetic progression has 3 as its first term. Also, the sum of the first 8 terms is twice the sum of the first 5 terms. Find the common difference. Find also the sum of the geometric series 8 − 4 + 2 − 1 + . . . where there are 5 terms in the series.

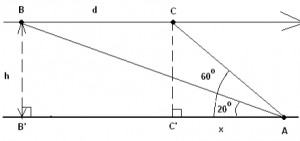
d- An airplane is approaching point A along a straight line and at a constant altitude h. At 10:00 am, the angle of elevation of the airplane is 20o and at 10:01 it is 60o. What is the altitude h of the airplane if the speed of the airplane is constant and equal to 600 miles/hour? (round answer to 2 decimal places).

e- Expand the logarithmic expression ln! �2+! �� , � > 0

f- A radioactive substance has a half-life of one week. In other words, at the end of every week, the level of radioactivity is half of its value at the beginning of the week. The initial level of radioactivity is 20 counts.
1- Draw the graph of the amount of radioactivity against time in weeks.
2- Find the formula that gives the radioactivity in terms of time.
3- Find the radioactivity left after three weeks.

g- The following data shows the number of people (in thousands) who own an apple cell phone device in Canada.

1- Determine an exponential equation that fits this data
2- If the increase in sales continues to increase at this rate, use the model to predict how many people will own a cell phone in 2025.
3- Determine the average rate of change between the years 2006 and 2010.

LO2: Investigate applications of statistical techniques to interpret, organize and present data by using appropriate computer software packages.

a- The owner of the Ches Tahoe restaurant is interested in how much people spend at the restaurant. He examines 10 randomly selected receipts for parties of four and writes down the following data. Find the mean and standard deviation 44, 50, 38, 96, 42, 47, 40, 39, 46, 50

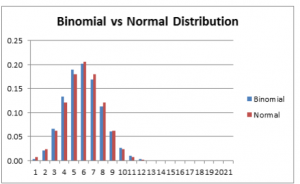
b- Show and explain what is the normal distribution approximation for the binomial distribution where n = 20 and p = .25 (i.e. the binomial distribution displayed in Figure 1 of Binomial Distribution)?

c- The average life of a motor is 10 years and the standard deviation is 2 years. Given that the manufacturer can replace only 3% of the motors for faulty reasons, how long should the guarantee be for if the lives of the motors represent a normal distribution?

d- The manufacturer of metal pistons found that on average 12% of the pistons are rejected because they are oversize or undersized. What is the probability that in any group of 10 pistons:
1- Not more than 2 pistons are rejected
2- At least 2 pistons are rejected
3- How would you interpret these results in terms of profitability and loss of revenues

e- The lifetime of a particular type of light-bulb has been shown to follow a Normal distribution with a mean lifetime of 1000 hours and a standard deviation of 125 hours. Three bulbs are found to last 1250, 980, and 1150 hours. Convert these values to standardized normal scores.

LO3: Use analytical and computational methods for solving problems by relating sinusoidal wave and vector functions to their respective engineering applications.

a- A system of solar panels produces a daily average power P that changes during the year. It is maximum on the 21st of June (day with the highest number of daylight) and equal to 20 kwh/day. We assume that P varies with the time t according to the sinusoidal function P(t) = a cos [b(t – d)] + c , where t = 0 corresponds to the first of January, P is the power in kwh/day and P(t) has a period of 365 days (28 days in February). The minimum value of P is 4 kwh/day.

1- Find the parameters a, b, c and d.
2- Sketch P(t) over one period from t = 0 to t = 365.
3- When is the power produced by the solar system minimum?
4- The power produced by this solar system is sufficient to power a group of machines if the power produced by the system is greater than or equal to 16 kWh/day. For how many days, in a year, is the power produced by the system sufficient?

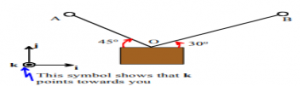
b- The figure shown in the diagram below is showing a heavy box that is suspended by two wires where OA is T1 and OB is T2. Represent the two forces T1 and T2 by their vector components using the directions given in the diagram.

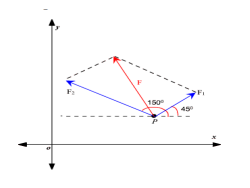
c- The two forces shown in the diagram below show two forces F1 and F2 and their values are 20lb and 30lb respectively. These two forces act on an object P as shown in the figure. What is the resultant force acting on the object?

LO4: Examine how differential and integral calculus can be used to solve engineering problems.

a- If two resistors with resistances R1 and R2 are connected in parallel as shown in the figure below, their electrical behavior is equivalent to a resistor of resistance R such that! . If R1 changes with time at a rate r = !”! !” and R2 is constant, express the rate of change !” !” of the resistance of R in terms of !”!
!” R1 and R2.

b- If an object with a speed v giving by the equation v ( t ) = 1 + 4t + 3 �! where t is the time taken to move per minute, what is the traveled distance during the third minute?

c- A wire of mild steel has a radius of 0.5 mm and a length of 3 m. If the young modulus Y = 2.1 x 10!! �/�! and the wire is stretched by a force of 40 N determine:

1- The longitudinal stress
2- The longitudinal strain
3- The elongation

d- If the switch ‘S’ is at position ‘1’ sufficiently long enough before it is moved to position ‘2’ and after this, it is kept in position 2 as shown in the figure below determine:

1- Values of the instantaneous inductor voltage �! and the instantaneous current through the inductor �!
2- Values of the inductor voltage �! and the current through the inductor �! just after the switch changes
3- The rate of change of �! at t = 0

Answer

Request Answer of this Assignment