- IF1201 Assignment: Developing Financial and Utility Tools Using VBA in Excel
- MA12009 Exploratory Data and Statistical Analysis of Airbnb and Spotify Datasets
- NVQ Level 5 Unit 507 Safeguarding in Adult Care
- Structural Design of a 4m Roof Beam: Load and Stability Analysis, Assessment 2
- M33118 Configuring and Studying ASA Basic Settings and Firewall Using CLI
- The Reasons For Hitler Gaining Power In 1933, Course Work
- Sensitivity Analysis of Option Pricing: Impact of Volatility and Barrier Conditions
- Network Threats and Vulnerabilities, UNIS, Coursework
- Corporate Finance and Business Valuation Coursework
- 5301ELE Digital System Evaluation Coursework, Level 5, LJMU 2024
- Power Electronic Applications and Control Coursework 1 2024
- PE7007 Construction Economics, Coursework Brief – 2024/2025 , NU, UK
- Level 3 Diploma in Adult Care, Coursework, UK: Understand the application of personcentred practices in care settings
- Decide whether each of the following statements is true or false. Justify your answer in each case by giving an example or stating any general result seen at the lecture: Mathematics, Coursework, NU, UK
- 7CO03: Critically assess different ethical standpoints on people practice and the maintenance of high standards of ethical behaviour: CIPD level 7 , Coursework, UK
- SQE2: Oral Skills-Written Skills- Apply the law comprehensively to the client’s situation, identifying any ethical and professional conduct issues: Reflective Portfolio, Coursework, UK
- SQE 1 Preparation: Portfolio Assessment-analyse and reflect upon your development of the practical legal skills that the Solicitors Regulation Authority (the SRA) : Reflective Portfolio, Coursework, UK
- DSM120: Financial Data Modelling, Coursework 1, UK
- DSM070: Building the Blockchain: the chain, mining, and the consensus mechanism: Blockchain Programming, Coursework 3, UOL, UK
- FHEQ Level 7 ES5800 – Systematic review protocol In this assessment you are asked to write a systematic review protocol: Analytical skills for Environmental Managers, Coursework, BUL, UK
EENG8760: This stretch of river can be modeled using a pure time delay model The transfer function of a pure time delay model in the Laplace: Advanced Control Systems Coursework, UOK, UK
| University | University of kent (UOK) |
| Subject | EENG8760: Advanced Control Systems |
Question 1
(a) This stretch of river can be modeled using a pure time delay model. The transfer function of a pure time delay model in the Laplace domain is given by
![]()
Let the time delay be r = 25 hours and assume the sampling interval, 7’s= 5 hours. Obtain the discrete state-space representation for this pure time delay model. State clearly the A, B, C, and D matrices. Show your detailed calculation.
(b) After you have obtained the discrete state-space model, augment the plant with the disturbance model using the following equations.
![]()
with 0 and I am respectively zero and identity matrices of appropriate size.
Question 2
(a) In Figure 1, the discrete transfer function of the integral controller, C(z) used to regulate the flow at Casey’s Weir is given by
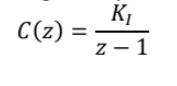
Let K, = 0.05, obtain the discrete state-space representation of this integral controller. Label the integral controller’s matrices as A1<, BK, CK, and DK.
(b) The city council require that the flow at Gowangardie Weir must be maintained at a minimum flow of 0.3m3/s for environmental purposes.
Suppose that the base flow of this river reach is at 0.6m3/s. Using the provided Simulink file, “Simulink ReachCG.sli’, let us assume farmers located close to Gowangardie Weir have a requirement to withdraw water from 105 hours onwards at 0.4 m3/s.
The integral controller is given in Question 2a) is to be used to restore the flow at Gowangardie Weir.
Question 3
(a) Given the imposed flow constraint, a Model Predictive Controller (MPC) has been proposed to replace the integral controller, as MPC has the potential to yield improved performance in the presence of constraints.
However, tuning the weighting matrices in the MPC cost function is often non-trivial.
One method to obtain the weighting matrices is to solve an inverse optimal control problem. In other words, we select a favorite controller Krav that is easy to tune and subsequently obtain MPC weighting matrices that can mimic Kfav by solving the inverse optimal control problem.
Using the full order observer method introduced in 7165MAA lecture week 5, obtain the weighting matrices (i.e. Q. R and S) that reproduce Kfav, i.e. the integral-controller given in Question 2 a). Show your detailed calculation.
(b) Run your updated “mpc ReachCG.nt, to design the MPC controller using the MPC weighting matrices obtained using the full state observer method, as computed in Question 3(a). Use a prediction horizon of 10. Compare and comment on the results of the MPC controller with those obtained using the integral controller simulated in Question 2(b), in the absence of constraints.
(c) Impose the output flow constraint set by the city council given in Question 2(b) in your MPC simulation. Critically assess and compare the performance of the MPC and I controllers.
(d) For MPC, in the presence of the output flow constraint, critically assess and compare the performance for the prediction horizon parameter set to 2, 5, and 10.
Do You Need Assignment of This Question
Looking for the best assignment writing online on EENG8760: Advanced Control Systems? then consult the experts of Students Assignment Help UK where our brilliant experts assist you to provide error-free and 100% plagiarism-free solutions on BTEC Assignment Help at a most reasonable price.



