A motor-pump assembly in a pumping station experiences severe vibration (may not be at resonance) when the motor operates: Acoustical and Vibration Engineering, Assignment, UOS, UK

A motor-pump assembly in a pumping station experiences severe vibration (may not be at resonance) when the motor operates at its normal operating speed of 2500 rpm. After a 1.5 kg un-damped absorber tuned to 2500 rpm is added to the part of the assembly, the system’s new natural frequencies are measured as 2492 rpm and 2509 rpm.

(a) What is the equivalent mass of the motor-pump assembly

(b) Determine the new absorber mass to change the system’s natural frequencies outside the range from 2440 rpm to 2535 rpm.

Question Two:

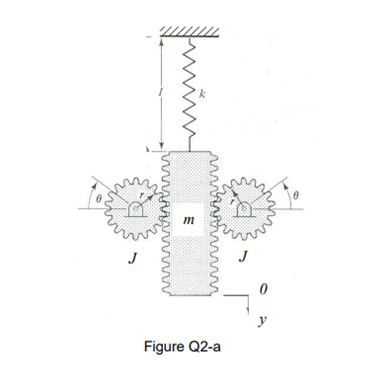
(a) An aircraft lift on an aircraft carrier can be modeled as a rack-and-gear system, shown in Figure Q2-a below. The mass of the spring is negligible. The system also consists of two identical gears of pitch radius r and centroidal mass moment of inertial J, a rack of mass At, and a spring of stiffness it

(a-1) Use Rayleigh’s energy method to derive the equation of motion of the vibration system with respect to the translational motion of mass M;

(a-2) Determine the system’s natural frequency.

Question Two:

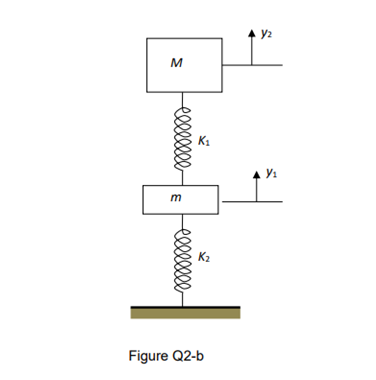
(b) A simplified vibration model for the chassis and suspension system of a car can be represented as a mass-spring system, shown in Figure Q2-b. M and m are the masses of the chassis and wheel assembly. lc, and k2 is the stiffness of the suspension spring and tires respectively.

(b-1) Develop a vibration model (equation of motion) for the system;

(b-2) Determine the dynamic matrix of the system.

Question Four

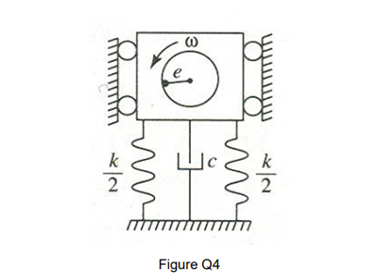
Figure Q4 shows a simplified vibration model for a machine of mass m mounted on a foundation which is modeled as a spring and damper system. The mass of the machine is 1500 (kg). The spring stiffness constant of the elastic foundation is k=60 (MN/m) and the damping coefficient is c-4000 (N-s/m).

The machine has an unbalanced component rotating at a constant angular velocity w = 205 (rad/s), which has a vertical component of the centripetal force off,(r)= 15 sin(ta) (N) acting on the machine.

(a) Derive the equation of motion of the vibration system;

(b) Determine the natural frequency and damping ratio of the vibration system;

(c) Derive the expression of the steady-state amplitude in terms of the natural frequency, damping ratio of the motion of the machine, and determine the steady-state amplitude of the vibration system;

(d) Determine the amplitude of the vibration dynamic loads acting on the base of the machine.

Answer

Request Answer of this Assignment